In collaboration with Tomáš Macháček
Code: github.com/ronaldluc/retail-bubble-stock-market-simulation
Stock market simulation
Introduction
In the past few months, the mania has taken over the world markets. Many countries have decided to use monetary expansion to battle the economic burdens of COVID‒19. This rapid increase of money printing has brought unusual amounts of money, especially to US households, resulting in quick asset price increases. First, the wave has taken over normal and rather safer assets, like Fortune 500 companies. After some time, the greediness of investors rose, and so did the proportion of money flowing into risky assets. As a result, we have seen rises in cryptocurrency and prices of small companies. In the end, many retail investors stopped investing and started participating in extremely risky strategies. This kind of behavior is present in the markets most of the time. The difference that made us take an interest in this was that usually, when these kinds of events happen, they tend to die out quickly, and there aren’t multiple assets getting “pumped up” at once. This time there were multiple assets over multiple markets with the same behavior, and the whole scheme did not stop for a couple of months.
Definitions
- Stock (Equity) — security that represents the ownership of a fraction of a corporation
- Investor — real-world entity buying equities
- Retail investor — individual, non-professional investor
- Momentum — velocity of stock price change over time period
- Price action — the price of the stock over time
- Pump and dump — is a scheme that attempts to boost the price of a stock through recommendations based on false, misleading, or greatly exaggerated statements
Problem formulation
How the overall strategies of investors and market parameters change the price action of stock during pump and dump events. Gains and losses with respect to the investment strategy. What seems to be the best investment strategy in these types of environments.
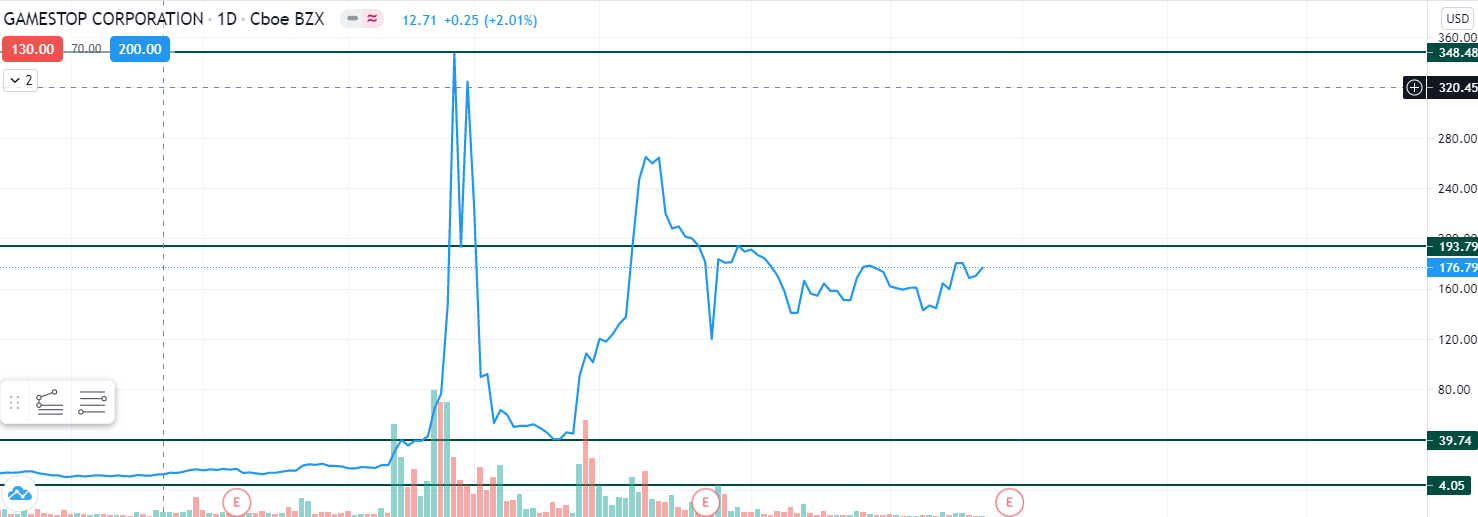
Source: own work
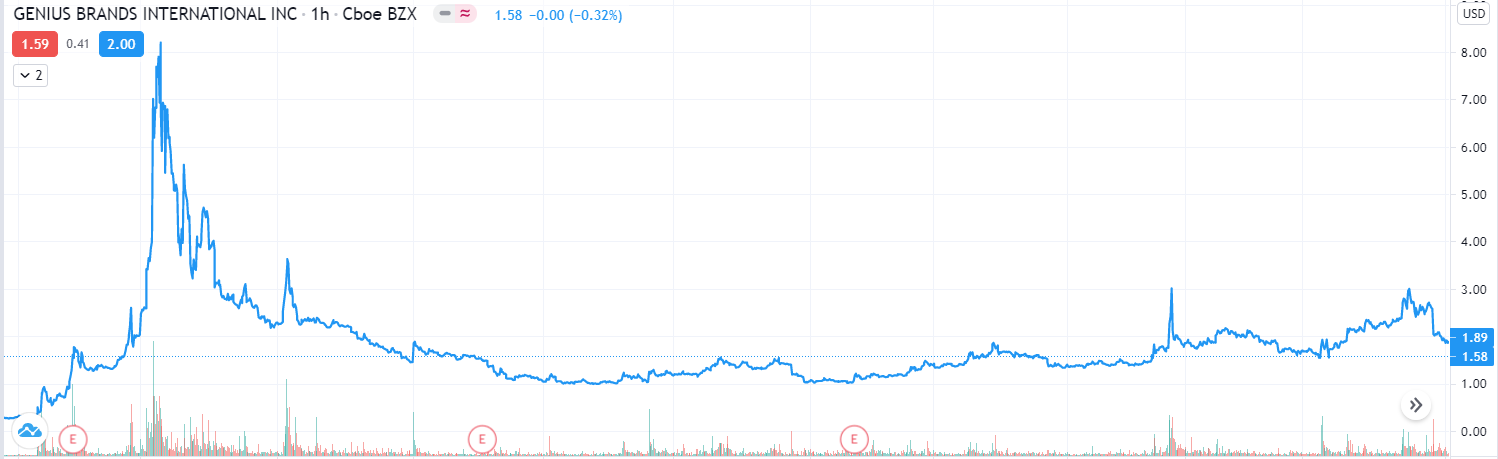
Source: own work
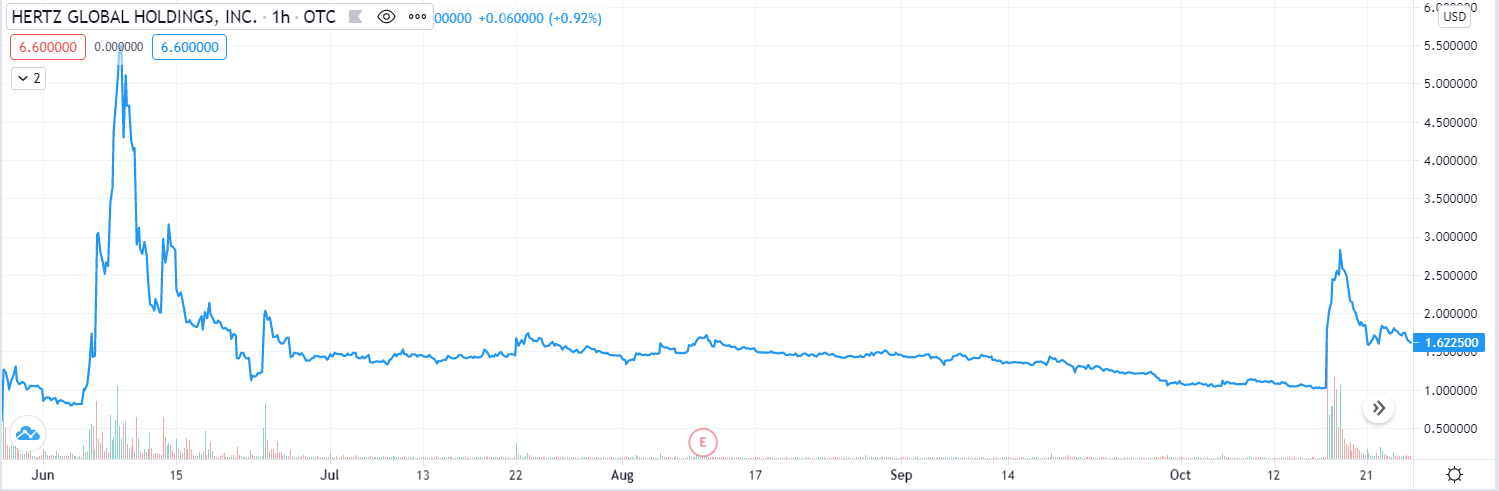
Source: own work
Real-life examples
In the real markets, pump and dump events are common occurrences. They usually occur on small, mostly worthless stocks. Usually, a small group of investors buy at a very low price and convince more investors to get in, with a vision of huge profit. This kind of thinking spreads like an epidemic since all of these new investors convince some of their friends to invest. This kind of behavior continues until most of the people willing to invest in this kind of scheme get in or until the hype dies out and people get bored, hence sell everything.
Model definition
In order to simulate the real market, we had to first create our artificial stock market. The price of the stock is simulated by an exponential curve with a very small base. Each tick of the model, investors may choose to buy or sell.
To buy
- At the start of each tick, the amount of money to be traded is calculated.
- Using a geometric sum, the total amount of shares to be bought is calculated.
- The shares are distributed between investors in proportion to the money spent.
- The new price per share is set, and the transaction is completed.
Likewise, to sell stocks.
For such stock market simulation holds
- All investors selling all stocks at once results in everyone getting a proportion of the current market cap.
- If the same investor solo-buys in one tick and solo-sells in the next, nothing changes.
- More generally, if investors sell in the reverse order to how they bought, everyone ends up with the same amount of money.
In the real stock market, price calculation works differently and depends on many variables that we are not considering in this model, such as share structure, spreads, and volatility.
We have decided to use an agent-based model for investors. Every investor starts with basic parameters that affect their trading decisions. In the beginning, there are only a couple of investors that are aware of the stock. Each tick, they have a small chance of telling someone else about the stock, hence spreading the hype. This so-called hype epidemic quickly spreads through all potential investors and causes the stock price to skyrocket since most of them wouldn’t want to miss on this investment opportunity. On the other hand, these investors are not stupid, and when the price is rising too quickly they have a chance to sell their shares. These decisions to sell and buy are based on investor behavioral function. The final factor contributing to our model functionality is boredom. After the scheme has been active for some time, some investors get bored and sell everything they have.
Behavior function
Behavior function is our way of representing the internal thoughts of an investor in a stock market. Every investor bases his decisions on his own parameters and the current stock price change, stock price delta. When the price is trending up or down slowly, most of the investors go along with the momentum; however, if the price starts rising or falling too quickly, some of the investors start thinking smart and do the opposite of what the rest of the investors are doing.
Input is delta_price (x-axis), ouput is buy/sell probability (y-axis). Best viewed with grid on full screen.
Hyperparameters
- “_exp” in name means the value is searched in \(10^x\) space
- name (range for search/substitution study): description
- ranges are chosen to be the wides reasonable (e.g., numerical stability in behavioral function)
Behavior hyperparameters
- mean_break_point_exp (-2, 0): mean of
breakdistribution - std_break_point_exp (-3, 0): std of
breakdistribution - std_optimism_exp (-3, 0): std of
optimismdistribution - behavior_scale (1, 50):
scale - behavior_linearity_exp (-1, 2):
linearity
Market hyperparameters
- past_impact_weight (1, 80): weight of history in
delta_pricecalculation - free_money_multiple (0.1, 100): how many times more money should all investors together have compared to the initial market cap
- stock_buy_extra_exp (-6, -2): additional price of the next share compared to the previous one ( \(share_{(n+1)} = share_n * (1 + stock\_buy\_extra )\) )
- transmission_prob_exp (-2, -0.9): a chance for each aware agent to spread the knowledge about to any other agent per tick
- boredom_prob_exp (-4, -2): a chance for each aware agent to get bored, sell all shares and never look back
- delta_price_exp (-6, 0): initial
delta_price
Feedback loop diagram
The backbone is a SIR model making an exponentially growing amount of people aware of the stock at the beginning
- S ~ unaware of the stock
- I ~ aware of the stock (and interested in investing)
- R ~ bored of the stock
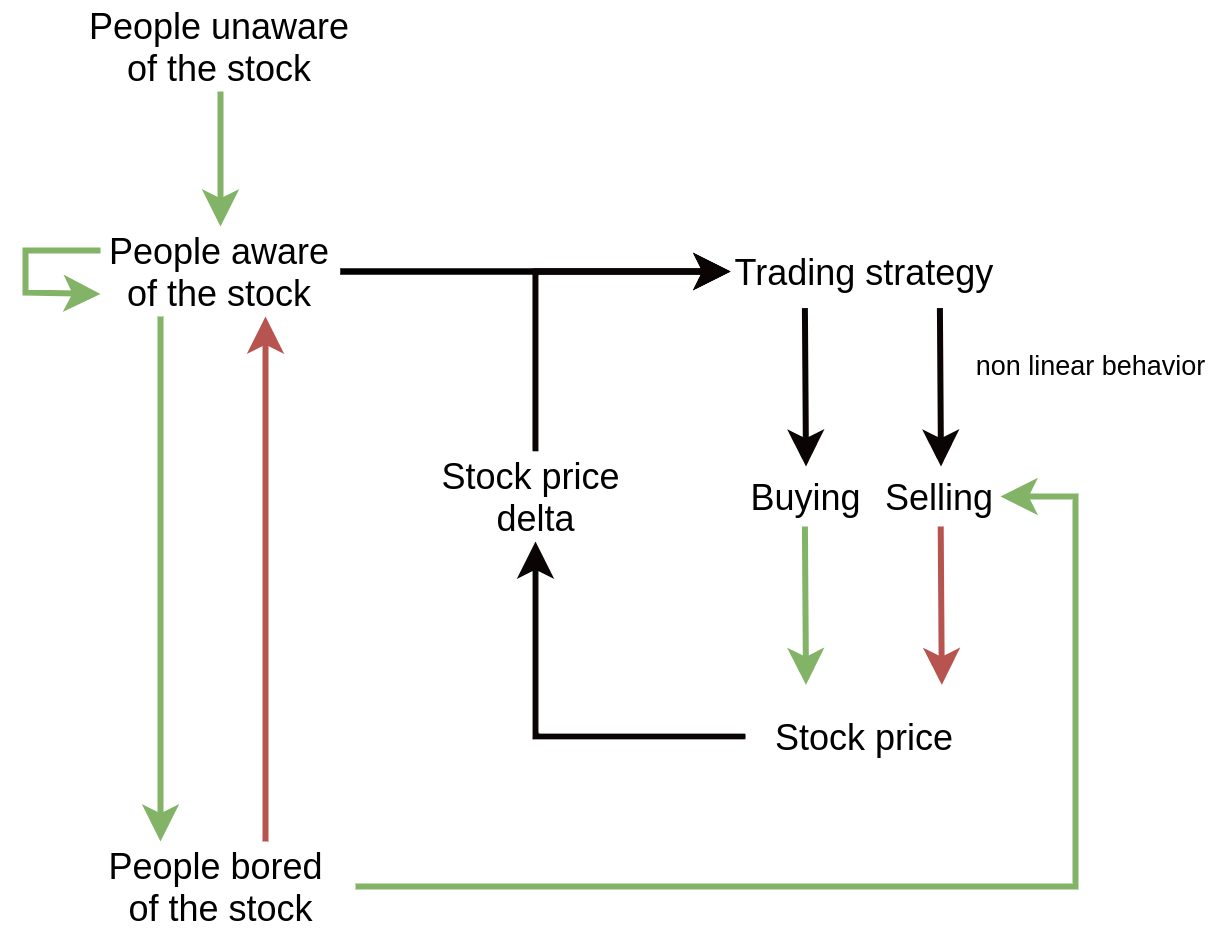
Source: own work
Evaluation
A single run
All values are normalized to <-1, 1> to be shown in one diagram.
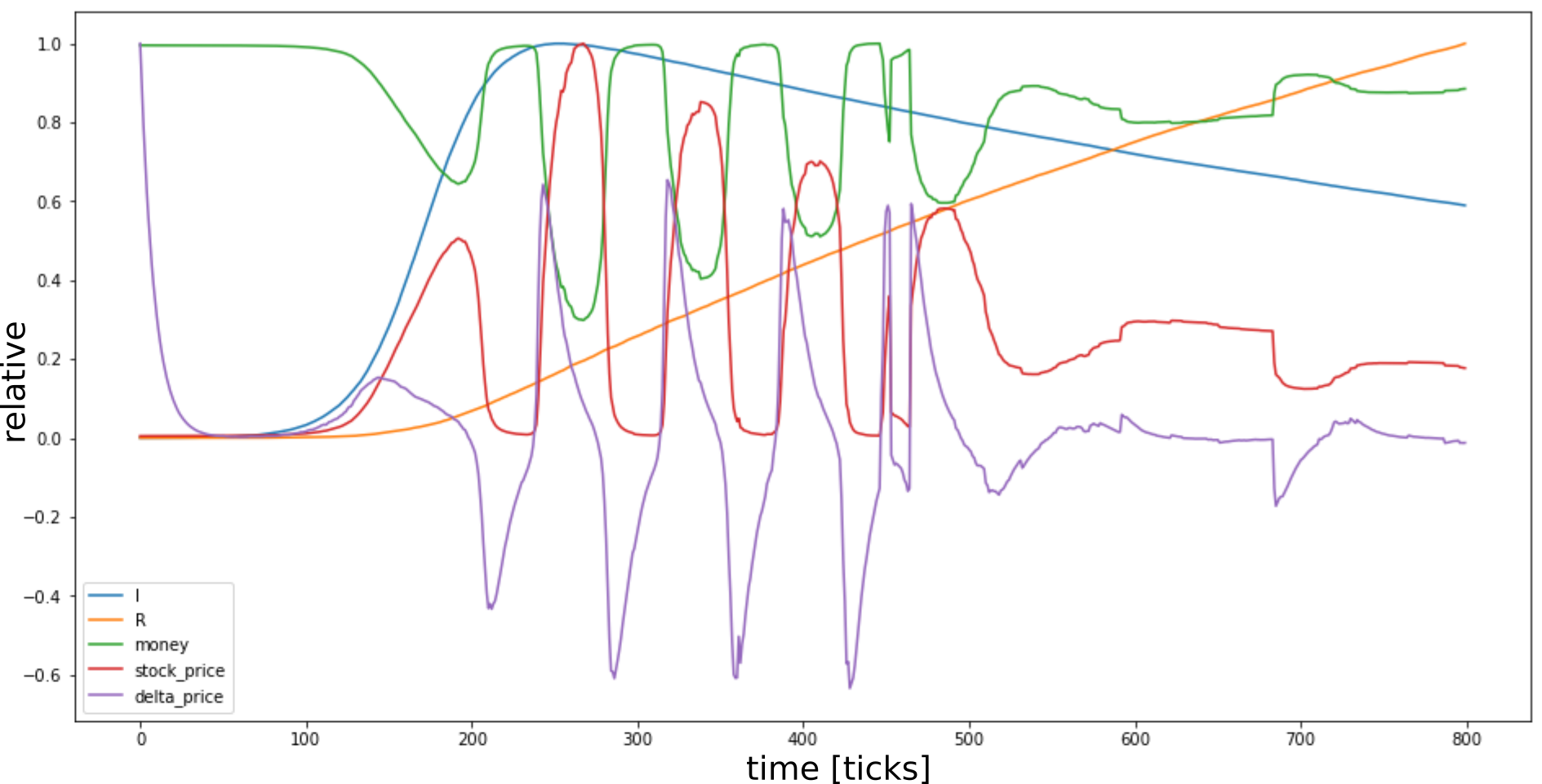
Source: own work
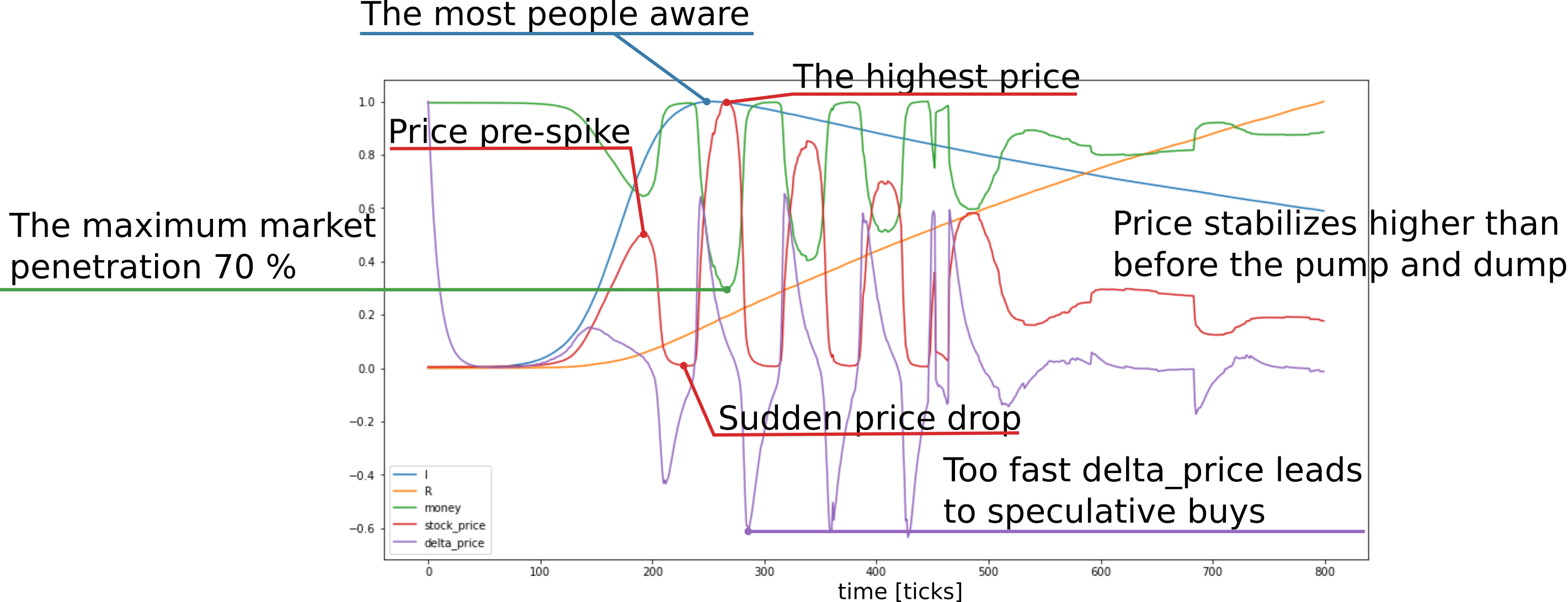
Source: own work
Selecting baseline
We want a set of hyperparameters that lead to models behavior similar to the one seen in reality. After analyzing a few pumps and dump stock price examples from reality, 4 peaks were chosen with ratios 2:4:18:9 and in-between drops with ratios 1:2:5. Those ratios were used to create a loss, for weights and implementation details see the ipython notebook.
GNUS pump and dump peak ratios examination
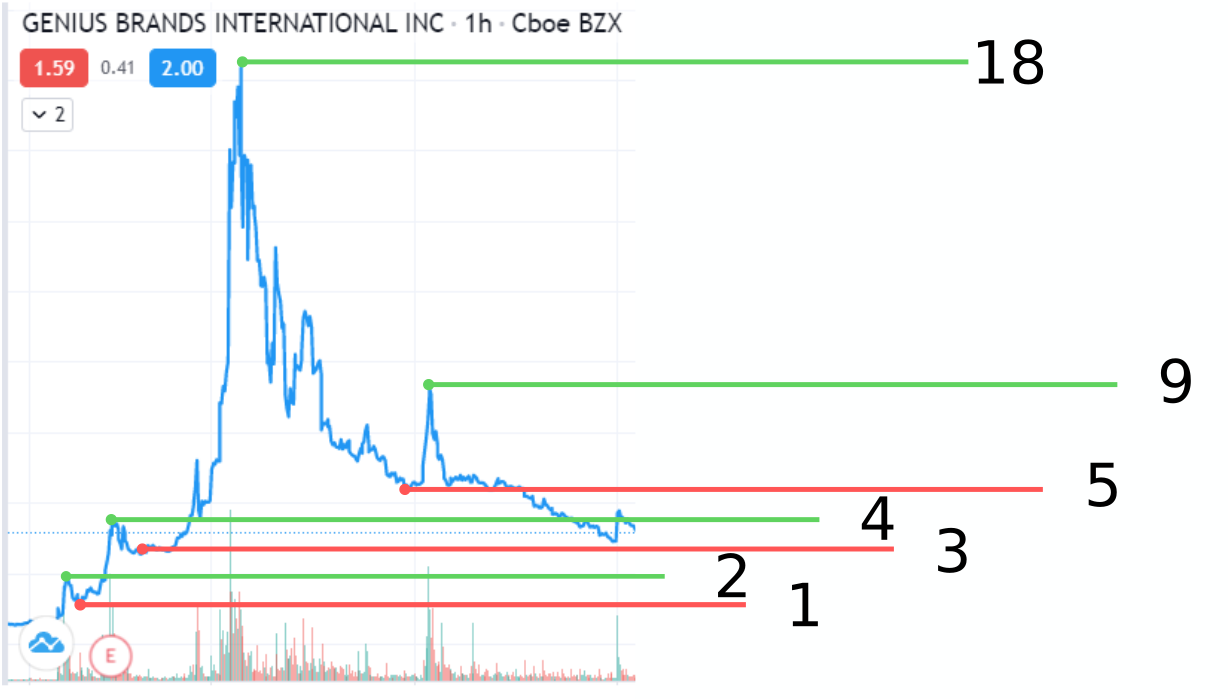
Source: own work
A hyperparameter search using bayes optimization with 3700 steps was used. The simulation is stochastic; therefore, each step is the average loss over 7 runs. The #1 in search is selected as the baseline.
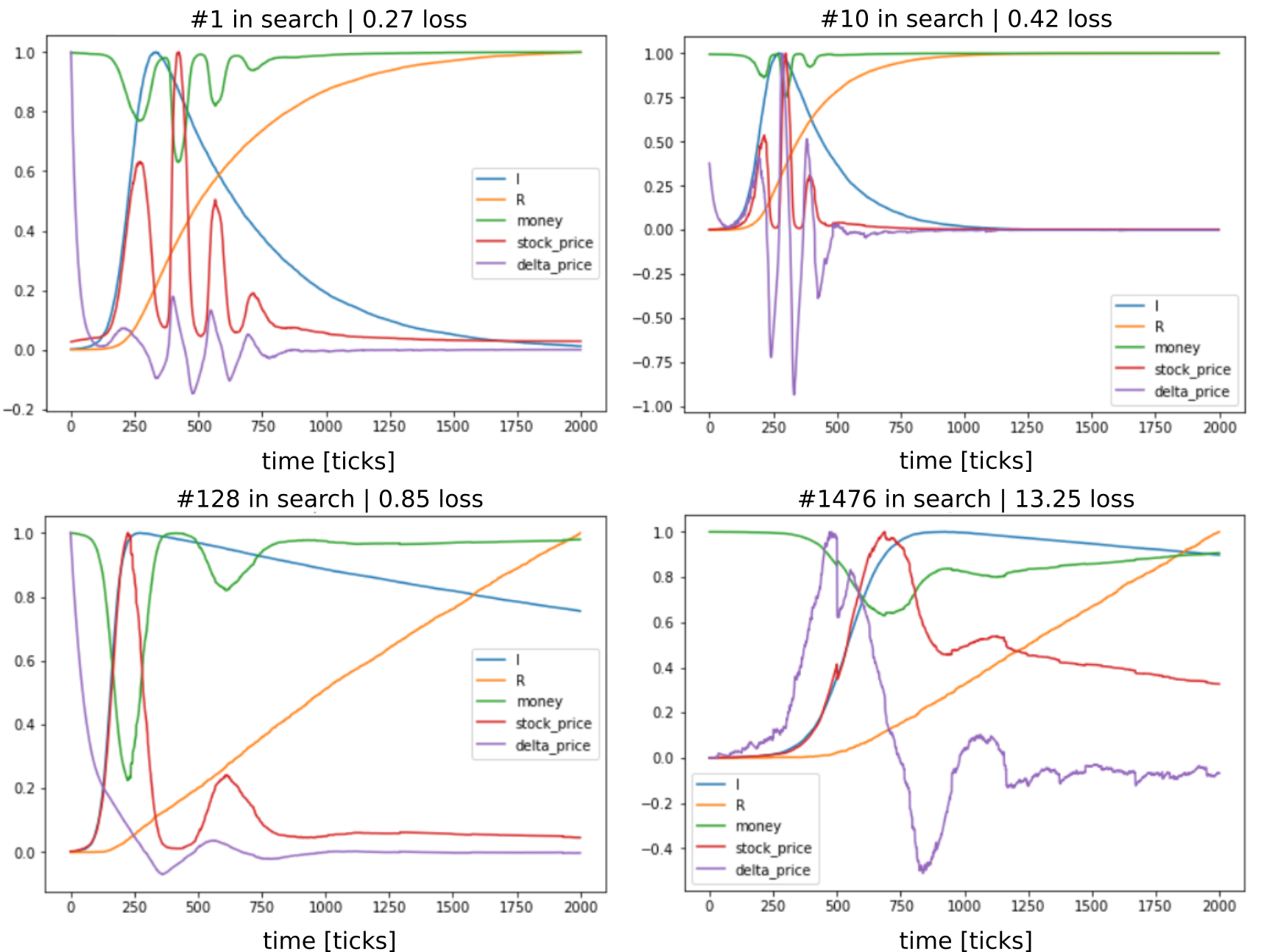
Source: own work
The models seems to be unable to perform 2 peaks before the main one. Then if there is a pre-peak, it is always around the linear part of I curve (awareness spread).
Abstracting the time
We are looking for the leverage points and phase transitions in the model. To achieve this, we create multiple market and agent markers. Each marker is a single number that represents a property over one market simulation.
Market markers
- first_peak [ticks]: tick of the first peak
- mean_peak [ticks]: mean tick of a peak
- last_peak [ticks]: tick of the last peak
- peaks_num [#]: number of peaks per simulation
- max_market_penetration [fraction]: the maximum fraction of money put into the stock at one time
Agent markers
- max_gain [money]: the most a single agent gained at the end of the simulation
- investore_lost_proportion [fraction]: the fraction of agents to end with less money than they started with
- money:optimism correlation [corr]: pearson correlation of the gained money to the optimism of agents
- money:initial_money correlation [corr]: pearson correlation of the gained money to initial_money of agents
- money:break_point correlation [corr]: pearson correlation of the gained money to break_point of agents
Each hyperparameter is evaluated on 1000 evenly spread values of a hyperparameter (x-axis). Shown is mean +- 2× std from rolling window of 50. Beware of relative y-axes.

Source: own work
Results
The most influential params
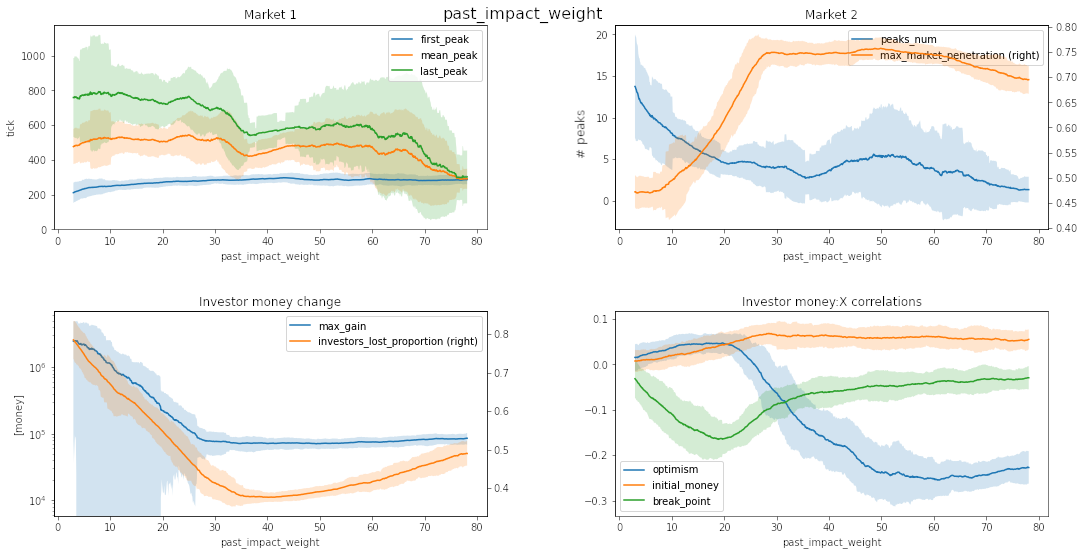
Source: own work
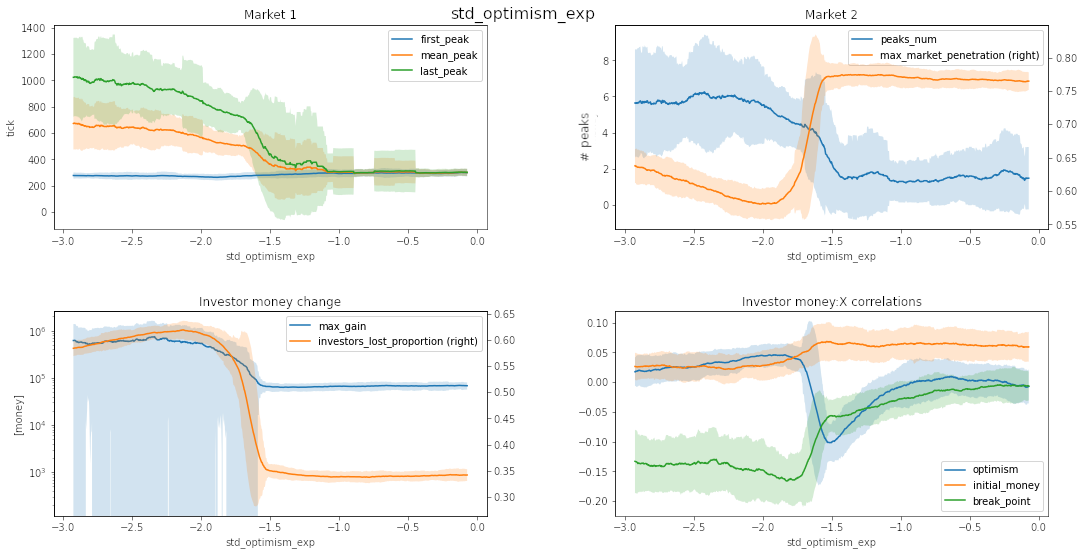
Source: own work
Changing past_impact_weight or std_optimism_exp makes the market penetration and money:optimism corelation undergo similar phase change. Worth noting is also the stable market behavior for any std of optimism over \(10^{-1} = 0.1\) (the optimism is always a normal distribution with 0 mean, so the change is done by a higher diversity in the optimism between people) with 1‒2 peaks.
Less influential params
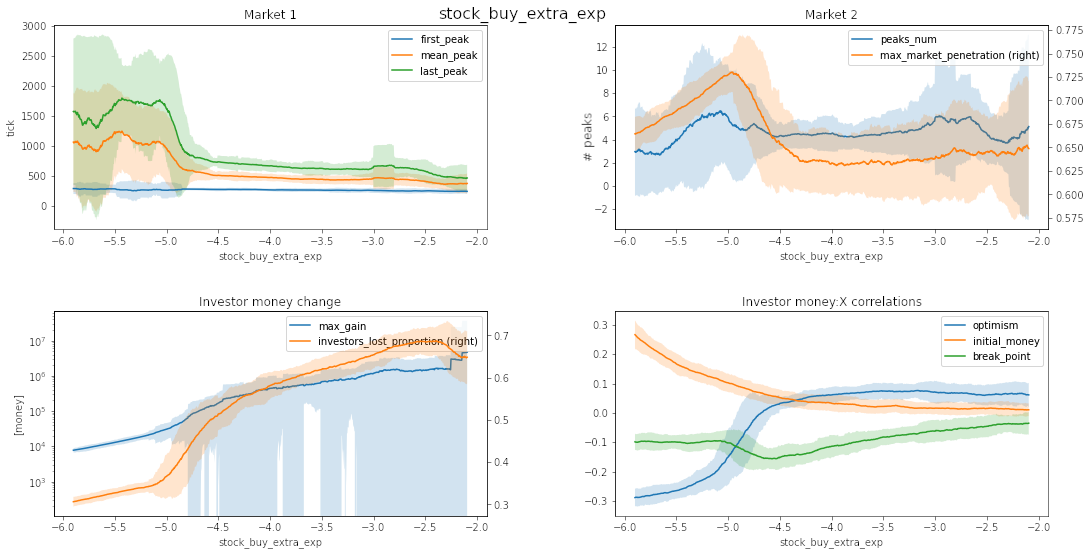
Source: own work

Source: own work
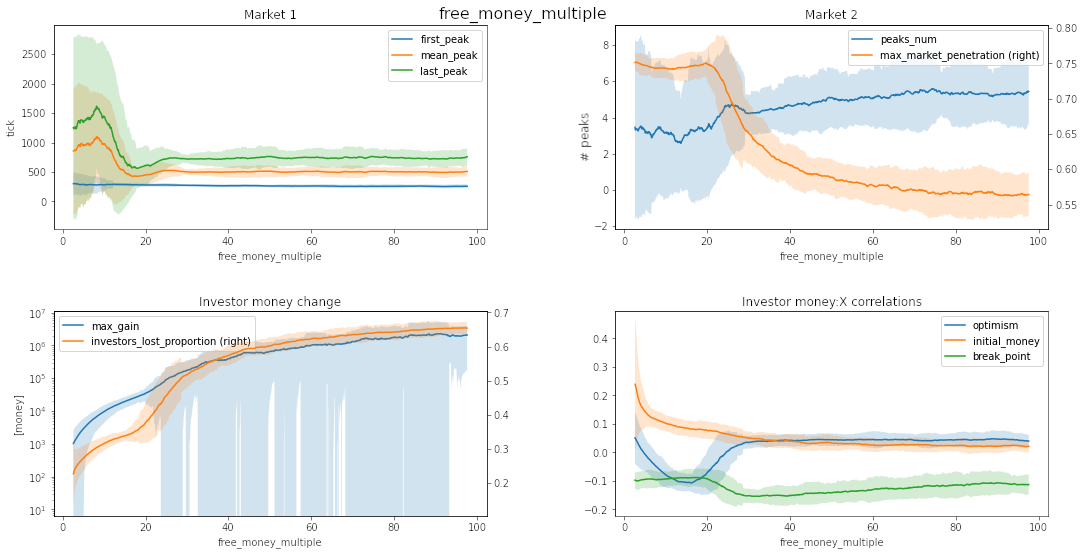
Source: own work
Changing free_money_multiple, behavior_linearity_exp, or stock_buy_extra_exp does not impact the market behavior much for most of the values used in hyperparameter search. If the free_money_multiple or stock_buy_extra_exp is small, agents cannot change the stock price too much \(\Rightarrow\) agents cannot gain/lose too much, and the money:initial_money correlation is high. Higher behavior_linearoty_exp increases the chance to trade \(\Rightarrow\) from a certain eagerness to trade the market behavior does not change much.
SIR params

Source: own work
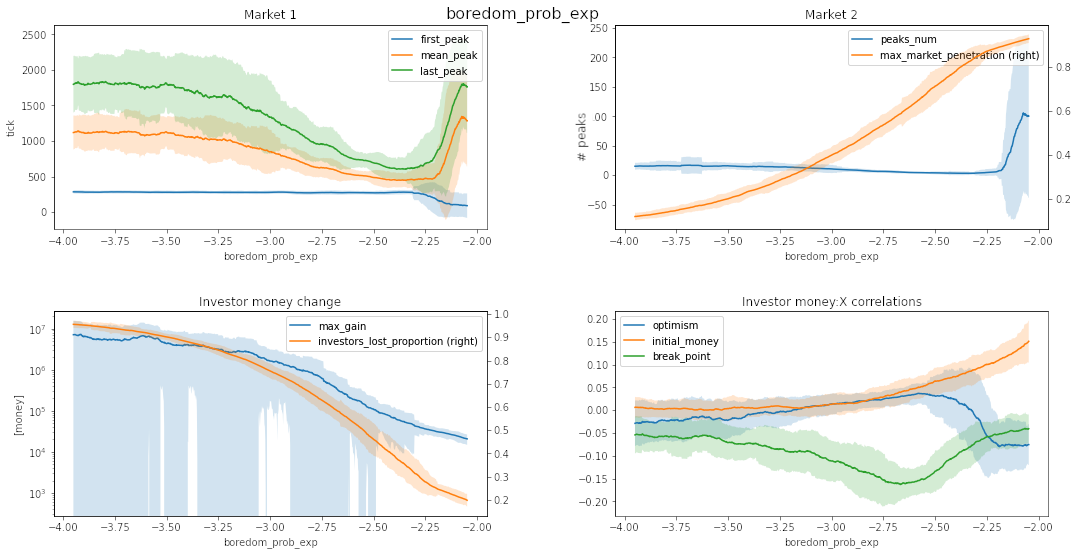
Source: own work
If the transmission_prob_exp, boredom_prob_exp are close together, the model oscillates a lot (hundreds of peaks). If the boredom_prob_exp is too low, not many people buy the stock, but the ones who trade are completely stripped of money by just a few agents. Changing transmission_prob_exp causes a phase change on money:optimism correlation \(\Rightarrow\) In a slowly spreading bubble, it is worth being a pessimist, and there are plenty of speculations (high # peaks), and most susceptible agents get involved. With quickly spreading hype, it is good to be slightly optimistic, and there are the same ~5 peaks before the meme stock is dead, with fewer people having time to get involved.
Break point
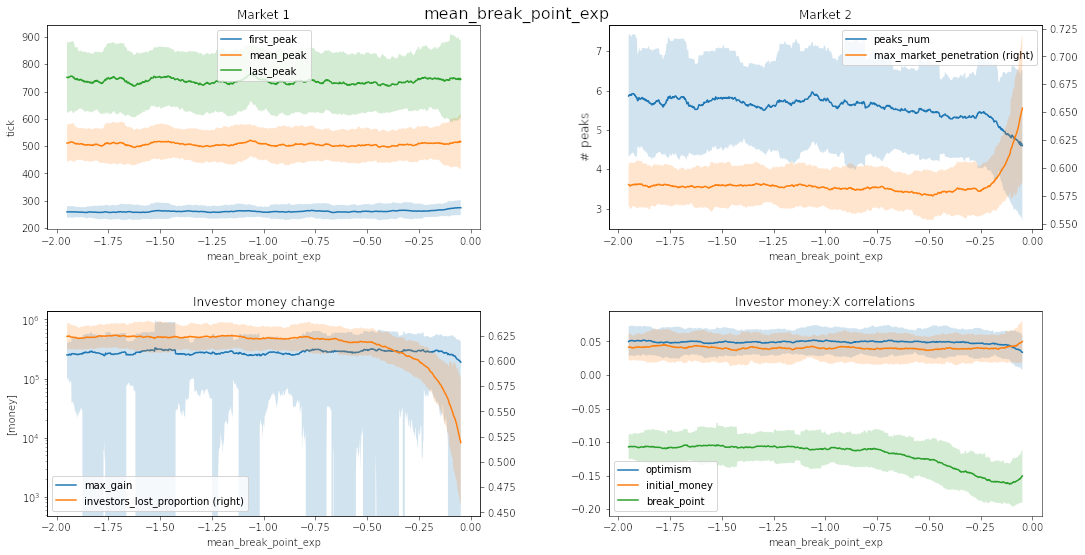
Source: own work
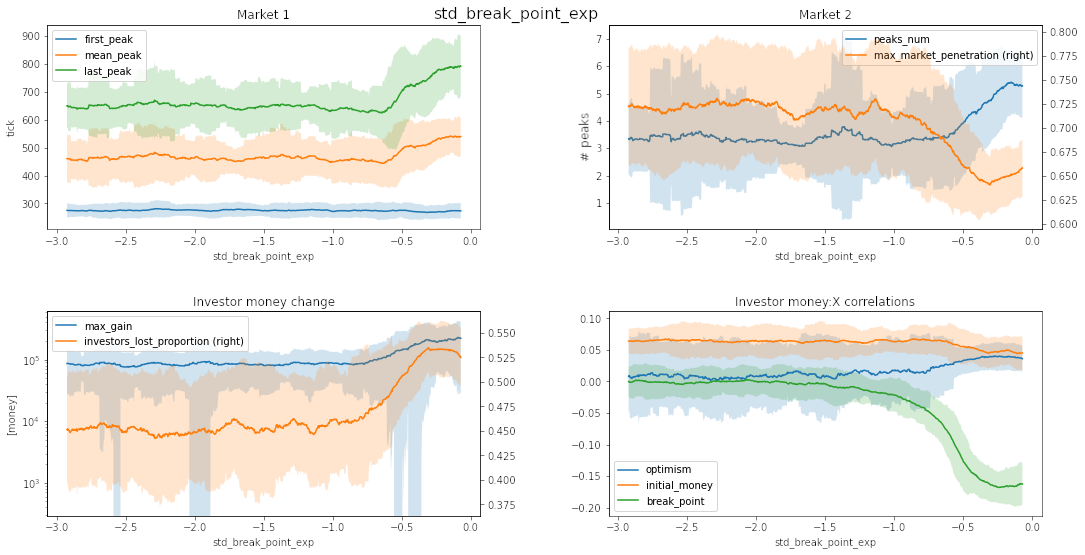
Source: own work
Based on the graphs shown, it might have been a good idea to search over an even wider range of break_point normal distributions. This was not done as break_point == 1 means a change in behavior only for delta_price > 1. With the search done, diversity in break_point is more important than the mean value.
No effect
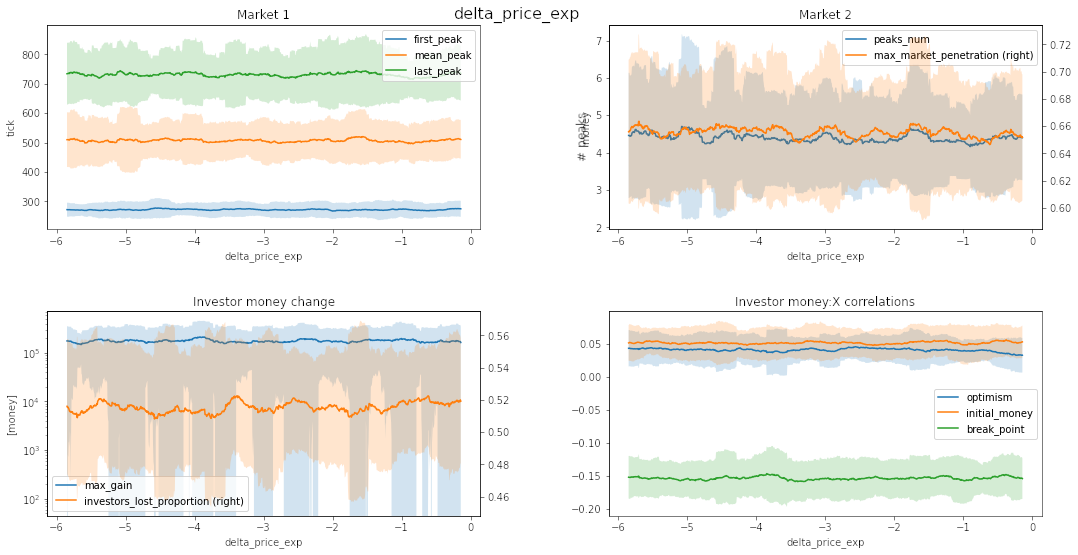
Source: own work
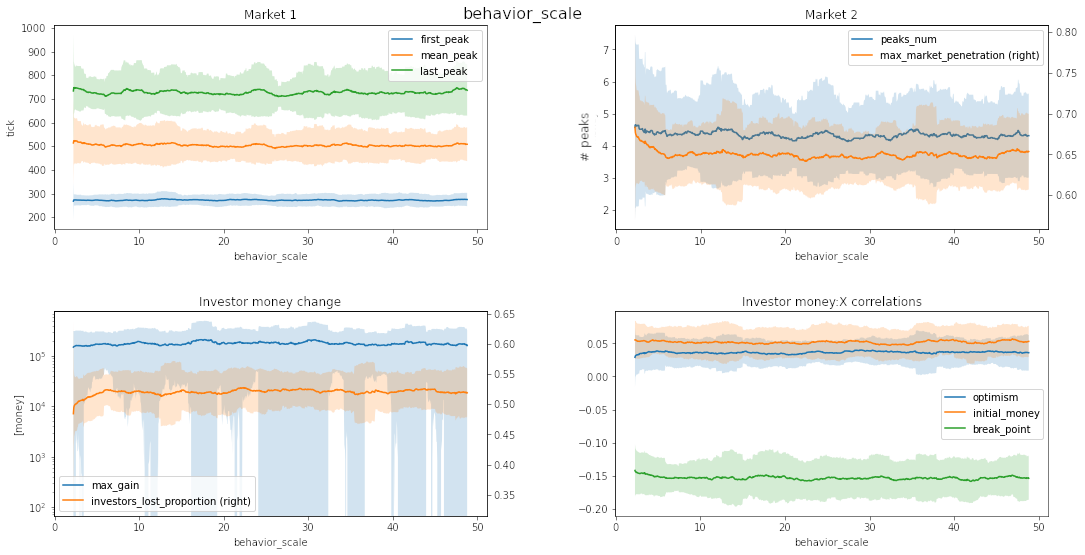
Source: own work
delta_price_exp and behavior_scale show little impact on the model behavior.
Conclusions
Overall, we were able to create a solid model that, with our level of abstraction, answered the questions we set out to answer at the beginning.
General questions about the market
Our first goal was to determine what are the most critical factors for the whole bubble to arise in the first place.
Looking back at past_impact_weight and std_optimism_exp, it becomes clear that these kinds of bubbles occur when people use the stock market as a casino. The two critical conditions for the bubble to arise seem to be the rash decisions, represented by low past_impact_weight where one looks only at low timeframes and herd mentality, represented by small deviations from base optimism. Even small changes in these parameters cause investors to act as if there was no bubble and the market was acting rationally. We can mostly see it in the past_impact_weight parameter, where even mid-ranged time frames simulate normal asset behavior. The best strategy in this type of market is to buy in and hold regardless of short-term events and price changes. We can see the same stabilizing effects with higher std_optimism_exp. In this case, it is less obvious why this stabilization happens. The point seems to be that more significant differences in personalities cause investors to act more rationally overall. When the stock goes up too quickly, pessimistic investors hold it down, so it can’t turn into a bubble, and optimistic investors buy even small dips, so the price cannot drop too quickly.
Our next goal was to determine which parameters contribute the most to investors losing money in these events.
Looking at our model and the real world, the basic answer to this question is that most people lose money because they risk. As we can see, the most influential parameters concerning the overall percentage of people who lost their money are the ones critical for a bubble to arise. From this, we conclude that participating in risky assets is what makes most people lose money.
Our model provides even more insight into this problem when we look at free_money_multiple'and stock_buy_extra_exp. These two parameters represent the two reasons for stock volatility. Higher free_money_multiple gives people more money, so they can get a bigger part of the company early on. This negatively affects overall investors because when these "whales" eventually sell their shares, they cause the market to crash on their own, hence hurt a larger amount of people in the process. stock_buy_extra_exp` has similar effects. In this case, the first investors get in at a low price and get a big share of the company, while the next investors get a disproportionally lower share of the company for the same amount. This again means that when the first investors sell, the crash inevitably happens.
Question about investor behavior
Our last goal was to look and try to figure out good strategies in bubble stocks.
We can’t fully answer this question using our simple model, but we can look at some interesting readings to try to determine the best behavior. First, looking at the critical conditions for the bubble to arise, we can see that optimism and cautiousness represented by low break_point positively predict success in the bubble market.
Next, looking at free_money_multiple and stock_buy_extra_exp, we can see that being optimistic in a low market cap environment is proficient.
Possible extensions
General market
- Price spread model
- Share structure model
- Model epidemic outbursts (stock mentioned in the news)
Investor behavior
- Add wealthy investors
- Change every parameter into a distribution sample for each agent
- Add more parameters into the behavioral function
TLDR
Taking into consideration what we had found out, the single best strategy is to never invest in assets with this behavior.


